10.什么是高中物理?-2
因为不让用微积分,无法处理复杂的变加速问题,我们就来分析一个最**一般的匀加速运动。一般**的意思就是:把它搞定了,其它所有情况就都搞定了。
一个典型的匀加速运动涉及5个物理量:初速度V0、末速度Vt、加速度a、运动时间t、运动距离S。
比如,一个苹果从树上静止下落,1秒后下落了5米,速度变成了10**m/s**。那么,这个过程中,初速度V0=0,末速度Vt=10m/s,运动时间t=1s,加速度a=g=10m/s²,运动距离S=5m。
我们关心的运动相关的物理量,就全部都在这里了。
接下来是重点:这5个运动相关的物理量,*任意已知*3个,我们都能求出另外的2**个。因为我们有2个显而易见的恒等式,5-3=2。**

第一个等式就是加速度的定义。你想想,加速度是什么?
加速度就是物体在单位时间(1秒钟)内速度的变化量。如果物体的初速度是1m/s,2秒后变成了5m/s,那它的加速度就是(5-1)/2=2m/s²,意味着它在1秒内速度会增加2m/s。
同样,如果物体的初速度是V0,经过时间t后速度变成了Vt,那物体的加速度a就可以表示为:a=(Vt-V0)/t。
整理一下,把t乘到左边,V0移过去。那初速度V0、末速度Vt、加速度a、时间t之间就有这样一个关系:Vt=V0+at(关系1)。
直观地看,加速度a是物体在单位时间内增加的速度,时间t后物体的速度就增加了at。那么,我用初速度V0加上增加的速度at,自然就得到了末速度Vt。
这本质上还是加速度的定义。
再看距离S,我们是如何求物体的运动距离的呢?
因为是匀加速运动,我们可以用初速度V0和末速度Vt的平均值(V0+Vt)/2当作整个运动过程的平均速度。
比如,物体一开始速度为0,1秒后速度变成了10m/s,那它这段时间的平均速度就是(0+10)/2=**5m/s。当然,这只在匀加速时成立,如果是变加速**就不能这么干了(为什么不能你可以想一想)。
好,知道了平均速度和时间,距离S就可以表示为它们的乘积,即:S=(V0**+Vt)×t/2(关系2)**。
这样,我们就有了两个固定的关系式:一个是加速度的定义,另一个是利用平均速度求距离:
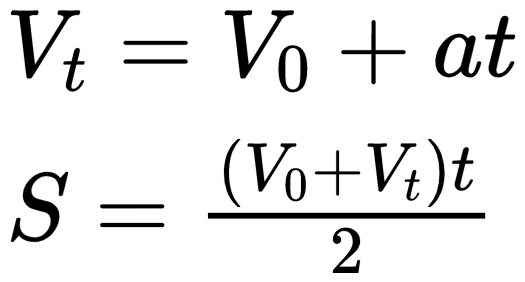
这两个式子的物理意义都很明确,容易理解。
有了这两个式子的神助攻,接下来,任意**已知3个物理量,我们都可以求出剩下的物理量**。

在学习物理时,为了加快解题速度,许多老师会让你背一堆公式。比如,已知V0、a、t,怎么求S啊,已知V0、Vt、a,怎么求S之类的。
但是我不建议你们这么做。
****
在学习物理时,我不建议你们在没有理解它的物理意义,没搞清楚它背后的物理图像之前死记硬背任何公式。
你想想,别说是上面两个物理意义很明确的式子,在给你讲万有引力定律时,我都没跟你说万有引力定律就长这样,你把它记下来就行了,要考。
我费了很大的篇幅告诉你为什么万有引力定律的分子会是两个物体质量的乘积,为什么引力会跟距离的平方成反比。
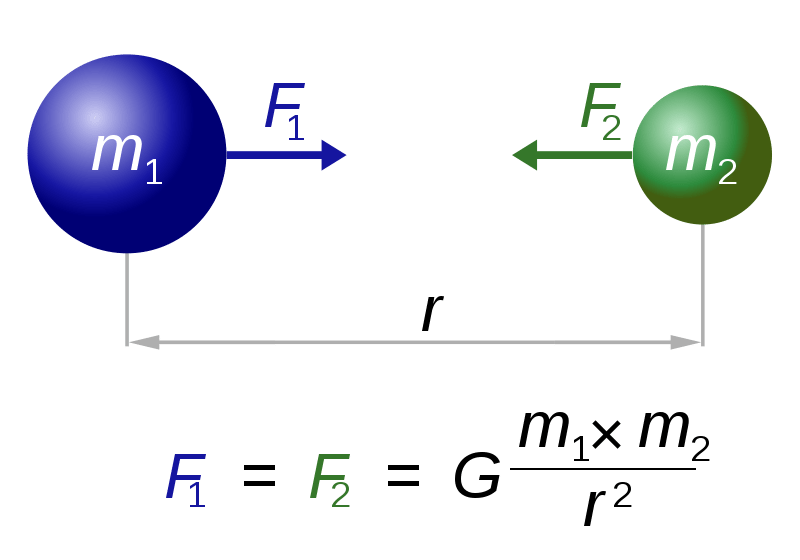
只有这样,你们才会觉得这些公式很自然,它们的物理图像很清晰。物理学原本就是描述自然界各种现象的,物理公式**自己会说话**。
好,我们现在知道跟物体运动相关的物理量就那么5个,有了那2个等式以后,其它关系式都可以从这里推出来。
比如,已知物体的初速度V0、加速度a、时间t,如何求运动的距离S**?这个场景非常常见,“苹果下落1秒后落了多远?”就是这种问题(V0=0,a=g=9.8,t=1**)。
那要怎么做呢?
很简单,要求距离S就得利用关系2(S=(V0+Vt)×t/2),这里V0和t都有了,就差一个Vt,而Vt可以根据关系1(Vt=V0+at)得到。
所以,最终的结果就是把关系1的Vt代入关系2,这样我们就能得到了一个不含Vt的关于S的表达式。
你亲自去推一下,就会得到这样一个结果:S=V0t+at²/2。
这个式子非常常用,但是我非常不建议你直接把这个公式死记下来,然后用它去套各种题目。
****
因为这个式子的物理意义不是很明显,你可以把这个式子记下来,但很难看清它背后的物理图像。
如果你把过多的精力放在记忆这种物理意义不明显的公式上,虽然短时间内能够提高解题速度。但长此以往,会逐渐丧失对物理图景的把握,会觉得物理越来越无聊,就是一堆公式游戏,那就完蛋了。
物理学是描述自然的,自然就在我们眼前,我们能看到,能感觉到。所以我们用来描述自然界的物理语言,也应该是能看到,能感觉到的。
****
我们学习物理,要尽力看清公式背后的物理图像,如果你觉得这些公式很简单,那物理就会非常简单。

因此,我整篇文章都在告诉你高中物理的框架是什么,如何看清它的物理图像。我想告诉你,物理学的每一种想法,每一个公式的来源都是有理有据有节操,合情合理又合法的。
关于物体的运动部分,我们只要知道描述物体运动的5个物理量之间有2个意义非常明确的关系式,其它公式都能从这里推出来就完了。
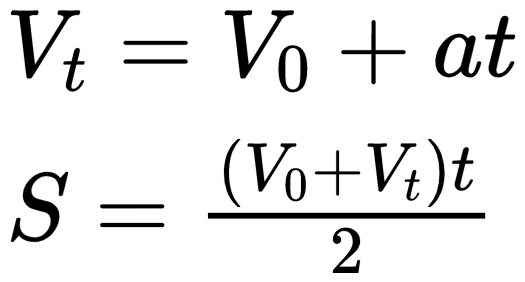
****
5个物理量,2个方程,你想推导不包含哪个物理量的方程,用消元法把它消掉就行了,不用死记它们。我们需要记住的是牛顿力学处理问题的一般方法,以及这背后的物理图像。
再回到上面的式子,不包含Vt的公式是这样的:S=V0t+at²/2。你需要这个公式时,临时推一遍就完了,耽误不了你多少时间。推导次数多了,很快就自然记住了。
你因为推导次数过多自然记住的,比死记下来的效果强太多了:第一,你永远不用担心会忘记公式;第二,作为出发点的那两个关系式的物理意义足够明显,所以你会觉得推导结论的物理意义也足够明显;第三,这个过程会锻炼你的逻辑推理能力,喜欢推公式的人,数学、物理都不会差。
这是一条通往学神的道路。

如果没有理清物理框架,没有看清公式背后的物理图像,只是死死地记住了一堆结论,记住了一堆特定问题的特殊解法,那物理会学得非常痛苦。
好,再来试一个,如果把时间t消掉,初速度V0、末速度Vt、加速度a、距离S之间就会有这样一个关系式:Vt²-V0²=2aS。同样,别去死记它,别把非常有意思的物理搞成了无聊的字母游戏。
本着这种精神,你会发现出题人在物体运动状态这一边能动的手脚也非常有限,无非就是在这几个量之间变来变去。
20场景复杂化
****
再回到核心的牛顿第二定律F=ma上来。
在这篇文章里,我坚持在牛顿第二定律后面加上了F=ma,如果你能看到这里来,看了这么多遍F=ma,应该形成条件反射了吧?
牛顿第二定律F=ma是整个牛顿力学的核心,它把物体的受力情况和运动情况联系在了一起,并且告诉我们物体受力之后要怎样运动。
围绕它出题,也只能一方面把物体的受力情况复杂化(添加各种各样的力,复杂化受力分析),一方面把物体的运动情况复杂化(V0、Vt、a、t、S五个量颠来倒去的变)。
如果还不够复杂,那就增加场景的数量。
比如,我让小球从光滑斜面上滚下来,这很简单。那好,我再增加一个场景:小球滚下来之后再经过一个摩擦力无法忽略的地板,在摩擦力的作用下慢慢减速。
还不够复杂?那我再增加一个磁场(电场),让小球滚进磁场(电场)里运动;加一个弹簧,让小球被反弹运动;加一个传送带……
于是,许多小场景就拼成了一个大场景,问题也就更加复杂了。这就像《猫和老鼠》里经常出现的一个机关触发另一个机关的场景,不停的运动。
架势看起来很吓人,但只要把每一个过程都分析清楚了,串起来的总过程也不会很难。

好,到这里,关于牛顿第二定律F=ma,关于力如何让物体运动的分析,就先告一段落。
从这种观点看世界,力处在最核心的地位。理论上来说,只要我们知道物体此刻的状态,知道它受到的力,我们就能根据F=ma算出物体后面任意时刻的状态(速度、位移都不在话下)。
牛顿也是根据这个,将上帝逐出了太阳系。决定物体如何运动的,将不再是上帝的意志,而是它受到的力。
因此,这种以“力”为核心观念的理论被称为牛顿力学也是非常贴切的。
接下来,我们换一种眼光看世界。
21另一种角度
****
从牛顿力学的观点来看,只要我们知道了物体的初始状态和受力情况,就知道了物体的一切。但是,理想很丰满,现实却很骨感,很多问题理论上可以计算,实际操作起来却复杂无比。
你想啊,牛顿力学的核心思想是物体下一刻的状态由上一刻的状态以及受力情况决定。这样,我们分析下一个状态,就要依赖上一个状态,而上一个状态又依赖于上上一个状态。
这就像多米诺骨牌,我们必须对物体运动过程中的每个状态都了如指掌才能给出最终的答案。
但是,很多时候我们并不关心物体运动的中间过程是什么样,我们只关心最后的结果。
又或者,我们根本没有能力(受限于观测水平、计算能力等)把中间过程完全搞清楚,但我们很希望知道最后的结果是啥样的。
比如,你经营一家超市时,很可能不是很关心每个月都有谁买了什么具体的东西。但是,你肯定关心这个月总共**卖了多少钱,进货花了多少钱,房租人力成本又花了**多少钱。
因为你知道,对于你来说:钱既不会凭空产生,也不会凭空消失(你没有能力印钱,也不会发疯去撕钱),它只会从一个地方流入到另一个地方(从买家手里流入你的手里,从你的手里流入上游供货商手里),但是总量保持不变。
好,现在我们发现了一条关于金钱流通的定律,我们姑且称之为“金钱守恒定律”。
有了金钱守恒定律,我们就不用知道每天每笔账的具体细节,只要知道了总收入和总支出,就能知道这个月赚了多少钱。

同理,大自然在不停地变化,物理世界也在不停地运动。那么,在这种运动和变化之中,有没有什么东西就像钱一样,也是变来变去但总量不变的呢?
比如,一个运动小球撞击一个静止的小球,撞击前只有一个小球在运动,撞击后两个小球都在运动,但是原来**小球的速度却变慢了**。
想想这个过程,似乎是原来的小球拥有一部分“运动”,撞击之后它把一部分的“运动”分给了另一个小球,然后自己拥有的“运动”就变少了。再多撞几次,它的“运动”就越来越少,于是它就慢慢减速,直到最后停了下来。
发现没有,小球失去“运动”的过程,跟我们失去金钱的过程非常类似。
我手上有一笔钱,给这个分一点那个分一点,然后我的钱就越来越少,最后没钱了。小球有一笔“运动”,它给这个分一点,那个分一点,最后“运动”分完了它就不动了。
金钱和“运动”如此类似,**既然有“金钱守恒定律”,那会不会也有什么跟运动相关的守恒定律呢?**
提到守恒就要比大小,几个量加起来等于另外几个量才叫守恒。
那问题的关键就是:金钱我知道如何衡量它的大小(直接用人民币的面额就行),那运动我用什么去衡量它的大小**呢?**
22运动的能力
****
一个小球以一定的速度运动,那它具有的“运动的能力”是多大呢?分给另外的小球之后,它们拿走了多少,我自己又还剩下多少?很显然,这些账必须算清楚,否则没法玩。
也就是说,我们现在需要找到一个量来描述小球运动能力的大小。这个量应该长什么样,我们不妨先来猜一猜。
很显然,最容易想到的就是速度。一个小球的速度越大,运动得越快,它显然就应该具有更多“运动的能力”。
但问题是,这种运动的能力跟小球的速度到底是什么关系**?如果小球的速度变成了原来的2倍,那它“运动的能力”到底是变成了原来的2倍,还是4倍、8倍**或者其它数字?
这种问题光靠脑袋是想不出来的,物理学是基于实验的科学,我们可以通过实验来寻找这种关系。
比如,我们可以让小球以一定的速度撞击其它的小球,再把小球的速度提高到原来的2倍、3倍,让它再去撞击同样的小球,看看它“运动的能力”到底提高了多少倍。

最后,实验结果告诉我们:物体具有的“运动的能力”,跟它的速度的平方成正比。
也就是说,如果速度变成了2倍,它具有的”运动的能力“就变成了原来的4倍;速度变成了3倍,后者就变成原来的9倍。
除了速度,物体具有的“运动的能力”显然还跟质量有关。同样的速度,一辆大卡车显然比一辆自行车具有更多“运动的能力”,前者明显能撞飞更多的东西。
同样的问题:它跟质量是什么关系**?**一个物体的质量变成了原来的2倍,它具有的“运动的能力”会变成原来的几倍呢?
同样的回答:去做实验,实验结果说什么,我们就听什么。最后,实验说物体具有的”运动的能力“跟质量成正比。
也就是说,质量变成2倍,”运动的能力“也变成2倍。
这也是很好理解的。因为质量变成了2倍,我就可以把它分成两个质量相等的小物体,这样每个小物体具有的“运动的能力”就应该和原来的一样,所以必然是2倍。
其它的因素好像暂时就无关紧要了。
这样,我们基本上就找出了物体“运动的能力”的定量关系式:它跟物体的质量成正比,跟物体的速度的平方成正比。最后,考虑到单位和数值,我们再加了一个1/2作为系数。
于是,这个定量描述物体具有”运动的能力“的物理量,就有了一个新名字:动能。
这个能,是能量(Energy)的意思,所以用字母E表示,动能就表示因为物体运动而具有的能量。
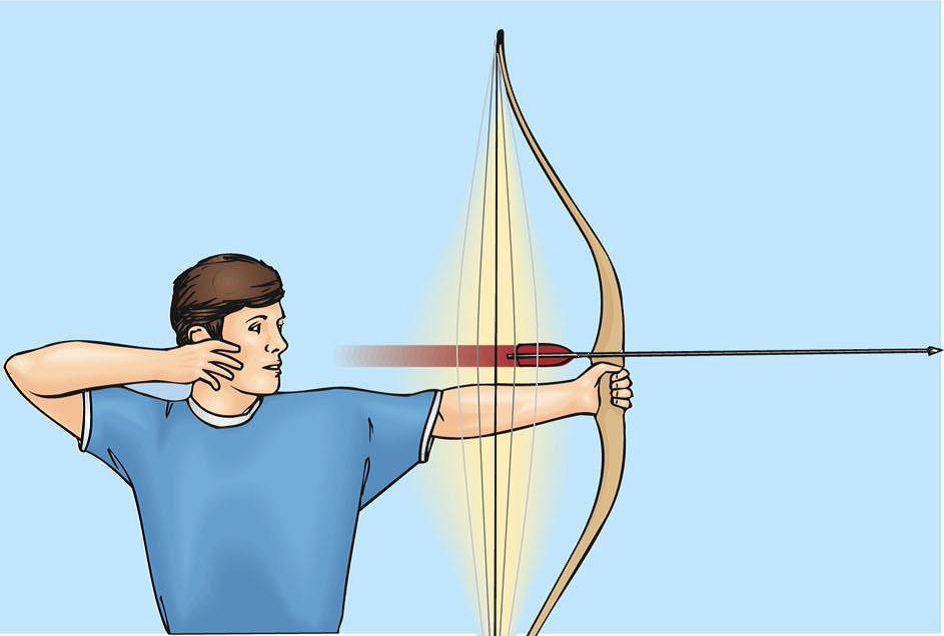
动能的大小就等于物体的质量m乘以速度的平方v²,再除以2,即:E=mv²/2。
有了动能的具体表达式,我们就可以对物体具有的”运动的能力“进行定量计算,算清楚后就可以和钱一样进行交易、分配了。
23能量守恒定律
****
动能,是物体因为运动而具有的能量,是能量的一种。
我们可以把这个能量分一点给其他的物体,中间环节我不管。你可以跟A物体关系好就给它多分一点,跟B物体关系不咋地就给它少分一点,但是能量的总和是一定的,**能量的总量是守恒的**。
这样,仿照“金钱守恒定律”,我们就有一条能量守恒定律:能量既不会凭空产生,也不会凭空消失,它只会从一种形式转化为另一种形式,或者从一个物体转移到其它物体,而能量的总量保持不变。
能量守恒定律是一条非常伟大的定律,它让我们有了另一种视角来看待物理世界,而且还很容易理解。
之前我们用牛顿**第二定律F=ma分析物体运动,它的核心概念是“力”。物体的运动状态之所以会改变,是因为有力作用在它身上。我们对物体进行受力分析找出合外力,然后根据F=ma求出物体的加速度,从而算出物体下一刻**的运动状态。
比如,一个运动的小球去撞击静止的小球,为什么静止的小球会动呢?
从力的观点来看,是因为运动小球跟它接触时,给它施加了一个力的作用。这个力让静止小球有了一个加速度,从而改变了它的运动状态。
你想算出静止小球后面怎么运动,就要算出它受**力**的大小。但是,这明显不太好算(就撞一下,我哪知道它到底有多大力啊,测也不好测)。
现在,我们有了能量的观点,就能从能量转化的角度来看这个过程。
为什么静止的小球会动起来呢?因为运动的小球把一部分动能给它了,于是静止小球就具有了一部分动能,就动了。
那么,静止小球获得了多少动能呢?答:原来运动的小球损失了多少动能,静止的小球就获得了多少动能,因为**动能的总量是守恒的(这里假设都是刚性**小球,碰撞过程没有能量损失)。
这样,我们就不用再关注碰撞过程中到底发生了什么,也不用去计算碰撞过程中每个时刻的受力大小,直接根据前后能量守恒就行了,这太棒了。
有了能量守恒这样一种新思路,科学家们高兴坏了。
这样,很多中间过程很复杂,但我们并不关心中间过程,只关心结果的问题就很好解决了。比如刚刚说的碰撞问题,用牛顿第二定律F=ma实在不好弄,但是用能量守恒就轻轻松松。
守恒律是物理学里非常重要的东西,为什么有些东西(比如能量)是守恒的呢?背后更深层的原因就是对称性。
比如,为什么能量守恒?因为我们的世界具有时间平移不变性。
简单的说就是今天有效的物理定律,明天也有效。把物理定律在时间上从今天平移到明天,它不发生改变(F=ma今天是这样,明天还是这样),这就是**时间平移不变性**。

你可能觉得这是废话,如果一条物理定律今天长这样,明天长那样,那我还要定律有何用?确实如此,如果物理定律天天变,那物理学也没啥意义了。
但是,正是因为有时间平移不变性,我们才有能量守恒。这个世界最难理解的事情,就是这个世界居然是可以理解的。这里就不多说了,感兴趣的可以看看我的这篇:《》。
好,发现了能量守恒这么好的东西,物理学家当然立马就被圈粉了,于是能量守恒就成了“物理正确”。
24能量的扩张
****
前面说了,刚性小球在碰撞时动能是守恒的,大家撞来撞去,动能就在它们之间不断流动。
但是,你观察苹果下落的过程:一个苹果一开始是静止的,这时动能为0。但是,它下落时速度在不断增加,所以动能也会不停地增大。
也就是说,苹果一开始动能为0,后来慢慢增大了。
不是说动能守恒的么?这里没看到其它物体动能减小,那苹果增加的动能是从哪里来的?为什么刚性小球碰撞时动能守恒,苹果下落时动能好像就不守恒了?问题出在哪?
我们想想,苹果之所以会加速下落,是因为地球对苹果有一个吸引力。这个引力让苹果加速,获得了动能。除了引力,还因为苹果距离地面有一定的高度,具有往下落的能力,所以才会加速下落,动能增加。
所以,面对苹果下落,动能不守恒这个问题,物理学家想到的办法是:苹果因为距离地面很高,而且受到重力,因此具有往下落的能力。这也是一种能量,我们把它定义为**重力势能**。
苹果在树上具有一定的重力势能,下落过程中,它的重力势能不断减小,动能不断地增加。虽然苹果的动能不守恒,但是动能和重力势能的总能量依然保持守恒。
这样,物理学家们深爱的能量守恒定律就依然成立。

同理,我们继续观察:一个木块在粗糙的地面上滑动,最后慢慢停了下来。那么,这个过程中木块的动能去哪了呢?好像也没有转化成重力势能或者其它物体的动能啊。
木块在粗糙地面上滑动时,受到摩擦力的阻碍而减速,这个过程加热了地面(摩擦生热)。
从微观来看,温度升高了,其实就是分子的运动程度变剧烈了,是分子的平均动能增加了。于是,我们又新定义了一种能量:内能。
因此,木块在滑动时,动能转化成了内能(或者说大量分子的动能),总能量保持不变,能量守恒定律依然成立。
同样,一个带电小球在电场中会被加速,动能增加。那这个动能从哪里来的呢?好,于是电场就理所当然地具有了能量,小球和电场的总能量守恒,能量守恒定律依然成立。
从某种意义上来说,能量守恒定律似乎永远不会错。因为你只要发现某个过程中能量不守恒,我就可以定义一种新品种的能量(就像重力势能、内能、电场能),从而让能量守恒继续成立。
25力与能量
****
力和能量是我们看待物理世界的两个不同视角。
面对同一个物理现象,你既可以对它受力分析,通过牛顿第二定律F=ma来求解;也可以找到系统的能量转换关系,利用能量守恒来求解。
那么,力和能量是怎么关联起来的呢?
看一个简单的例子:我用一个恒力F(大小和方向都不变)去推一个质量为m的静止物体,然后物体均匀地加速到速度v。
从力的角度看,物体受到的合外力就是F,它在这个力的作用下产生了一个加速度a,然后物体以这个加速度从静止加速到速度v。
不知道大家还记不记得前面关于运动部分的分析。5个运动相关的物理量V0、Vt、a、t、S,我们只要知道3个,就能求出另外2个,因为有两个恒等式:
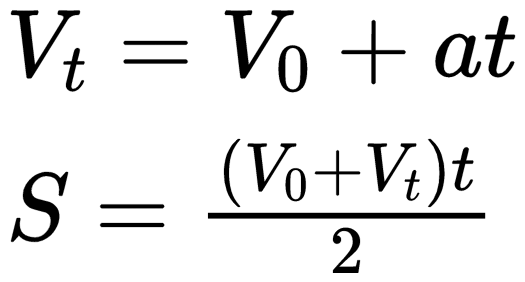
在这个例子里,我们已经知道了3个物理量:初速度V0为0,末速度Vt为v,加速度为a。
利用上面两个关系式消去时间t,我们就能得到其它四个量的关系:Vt²-V0²=2aS。在这个例子里,V0=0,Vt=v,代入进去就是v²=2aS,于是距离S就可以写成:S=v²/2a。
把距离S求出来干嘛呢?我们不妨来算一算力F和距离S的乘积F·S,也就是算一算力F在空间上的累积。
为什么要算这个量呢?待会儿你就知道了。
因为S=v²/2a,力F可以根据牛顿第二定律**F=ma来算,那么力F和距离S的乘积F·S**可以表示为:
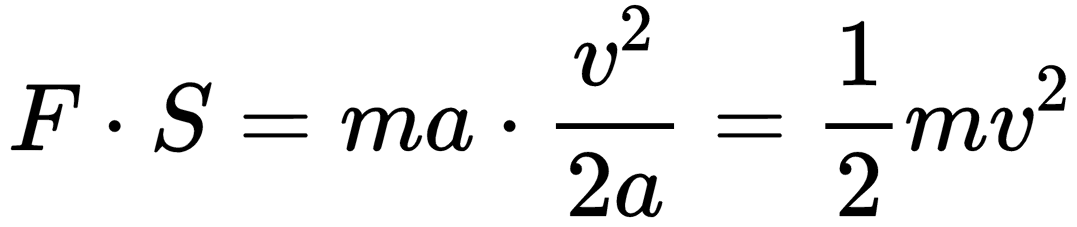
看到没有,这两个量相乘,刚好把加速度a约去了,剩下的结果竟然就是mv²/2。
有没有很眼熟?这不就是刚刚说的物体的动能么?
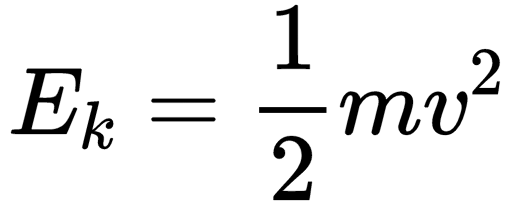
也就是说,我们用力F乘以这个力作用的距离S,得到的结果竟然跟物体后来的动能一模一样。
这是一种巧合,还是有什么更深层的含意?

好,上面我们从“力”的角度分析了这个过程,下面再从“能量”角度来看看。
从能量角度来说,物体一开始是静止的,动能为0,后来具有速度v,动能为mv²/2。
也就是说,物体凭空多出了mv²/2的动能。那么,这个能量是从哪里来的呢?
从直觉来看,物体会动,是因为有一个力F在推它。那么,这个力又是从哪里来的呢?
如果是一个人在推物体,那么,为了使出这个力,这个人肯定需要消耗一定的能量。其中一部分能量就给了物体,成了它的动能。
如果是地球在吸引物体,那这个F就是重力,结果就成了重力势能转化成了物体的动能。
如果是一个电场在推物体,这个力F就是电场力,这个过程就是电场能转化成了物体的动能。
当然,题目并没有说这个力F是从哪里来的,我们也就无法知道到底是什么能量转化成了物体的动能。
但是没关系,不管这个力是什么力,也不管这个能量到底是从哪转化来的,我们只要知道用这个力F乘以距离S就能等效地算出这个动能的大小就完了。
力作用在一个物体上,并且使物体在力的方向上移动了一段距离,这个过程在物理上叫做功。它是能量从一种形式转化为另一种形式的过程,正如上面人的能量、重力势能、电场能转化成物体动能那样。
虽然这个概念很重要,但是我现在并不想过多地讲这个。你脑袋里只要有清晰的能量守恒、能量流动、能量转化的图景就完了。
有了“力乘以距离就能等效地算出这个动能的大小”的概念后,你会发现很多能量的公式根本不用记,自然而然就能写出来。没错,我一直在教你“自然而然的物理”,教你如何不去死背物理公式~
26不用死记的能量
****
比如,一个质量为m的苹果,在高度为h的树上,它具有的重力势能是多少?
苹果从树上静止下落,从能量角度来看,就是苹果具有的重力势能转化成了它的动能。而我刚刚说了,力F乘以距离S就能等效地算出这个动能的大小,那自然也就算出了重力势能的大小。
在地面附近,苹果的重力为mg,它从苹果树下落到地面要走的距离为h。那么,用重力乘以距离得到的mgh,自然就是苹果具有的重力势能。
同样,在一个匀强电场E里,电荷q受到的电场力为qE。那么,在高度为d的地方具有的电场能就应该是qEd。不过,出题人一般会告诉你电势差**U=Ed,这样电场能就可以直接写成qU**。
弹性势能稍微麻烦一点,因为弹簧被压缩时,弹力的大小F是一直在改变的F=-kx(k为弹性系数,x为压缩距离),并不像重力mg、电场力qE那样一直是恒定的。
因此,我们就不能直接用一个固定大小的力乘以距离来表示弹性势能。而应该把弹簧分成很多片,在每一小片里近似认为弹力不变,求出这一小段的弹性势能,再把所有的加起来。
这又是微积分的思想,你看看我这篇《》,就知道怎样利用弹力公式F=-kx来计算弹性势能的大小了(提示,最终弹性势能的表达式为kx²/2)。
知道怎么表示重力势能以后,我们再来看看苹果下落这件事。
假设苹果的质量为m,苹果树的高度为h。在树上,苹果的动能为0,重力势能为mgh;苹果落地时,重力势能为0(因为高度h=0),动能达到最大的mv²/2。
因为能量是守恒的,所以在树上的总能量(0+mgh)就应该等于落地时的总能量(mv²/2+0),即:
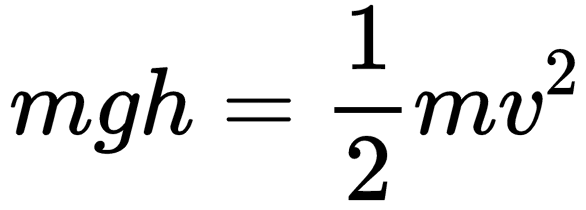
把质量约掉,g又是一个常数,这个式子就变成了高度h和落地速度v的一个关系式。很显然,已知其中一个,立马就能算出另外一个。
当然,如果知道了树的高度h,就等于知道了运动距离S,加速度又是已知的g,初速度等于0。所以,我们就已经知道3个运动相关的量了,从运动学关系出发,一样可以算出下落时间t和落地速度v。
这是两种不同的视角,两种方法也都不难。
27能量视角的优势
****
再看一个有区分度的:
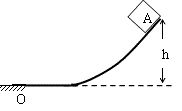
一个物体从一个弯曲的光滑斜面往下滑,注意斜面不是平的。因为弯曲,所以物体在不同时刻沿着斜面方向的分力是不一样的,因此物体的加速度也在不停地改变。
就像我们滑滑梯时,都是一开始坡度大一些,加速度大一些,后面平缓一些,加速度小一些。

这样你再想从力的角度对它进行运动学分析就困难了吧?因为物体的加速度一直在变,这是一个变加速运动。
更麻烦的是,题目压根就没告诉我这个曲面是怎么弯曲的,这样就求不出中间时刻的加速度,那速度自然也没法求了。
但是,从能量角度来看,这个问题跟苹果下落的问题没有任何区别:都是静止物体从某一高度下落,重力势能完全转化为动能的过程。
所以,从能量守恒的角度,我根本就不需要知道这个斜面是怎么弯曲的,不需要知道中间过程都是啥样。
我只要知道,最后到达地面时,它全部的重力势能mgh都转化成了动能mv²/2就完了:
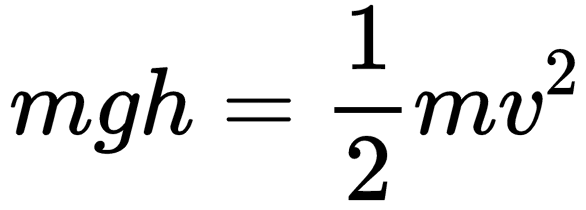
你看,整个方程都跟苹果下落一模一样,非常简单。
这样,大家对能量视角有什么新体会么?
28物理学的图像
****
说了这么多,我都在说些啥呢?仔细想一想,似乎这篇文章从头到尾都在教你不要死记物理公式**,不要硬背物理定律,要看清物理学的图像**。
物理学是一门研究物质基本运动和规律的学问,牛顿力学又是极其成熟的一套体系。既然非常成熟,那它自然就有一套非常完善地处理各种问题的一般方法。因为自成体系,所以它也有着清晰的框架结构和逻辑基础。
我写这篇文章,就是希望能帮你把这套体系理清楚,让你知道牛顿力学眼里是如何看待这个世界的,它处理物理问题的通用框架又是怎样的。
我不希望学生们一到高中就迷失在各种物理技巧和细节的海洋里,然后直到高中毕业,脑袋里都没有一块完整的物理学拼图。

牛顿力学和原来物理学的一个最大区别就是:牛顿力学认为力不是维持物体运动的原因,而是改变物体运动速度的原因。这种思想在牛顿第二定律F=ma这里得到了完美的体现,所以牛顿第二定律这么重要。
F=ma不就是在告诉我们力F是如何改变物体的运动速度(加速度a)的么?然后,你是什么力(引力、摩擦力、弹力、电场力),找到描述这种力的公式就完了;它要怎么运动,无非就是V0、Vt、a、t、S这五个运动物理量之间的字母游戏。
能量和能量守恒则提供了另一种看待问题的视角。
这里不需要力,我们只要抓住各种能量之间是如何转化的,就像抓住经济活动中金钱是如何流动的一样。只要把逻辑理清楚了,许多能量的表达式都是非常自然的。
“力”这个概念在高中随处可见,但基本上也就局限在牛顿力学里了,它是牛顿力学这个特定背景下的产物。当你以后学习近代物理时,你会发现力的概念越来越少,现代物理里甚至通篇没有“力”这个东西。
但是,能量的概念在牛顿力学、相对论、量子力学、量子场论里一直都有,它是超越牛顿力学,在所有物理学里都非常重要的存在。
好,回到牛顿力学,我们再来聊最后一个话题。
29从牛顿第三定律出发
牛顿力学有三大运动定律,它们是这个体系里最基本的东西。第一定律(惯性定律)和第二定律(F=ma)我们已经很熟悉了,牛顿第三定律的存在感没有那么强,可能是因为它太“显而易见”了吧。
但是,从它“推导”出来的一个东西却非常有意思,我们一起来看看。
牛顿第三定律简单的说就是:相互作用的两个物体作用力和反作用力大小相等,方向相反(牛顿的原话是“每一个作用都有一个相等的反作用”,并没有提到力。但因为我们学的是牛顿力学,所以教材里都直接用作用力和反作用力来表述)。
举个例子,你用力推墙,就会感觉墙也在以同样大小的力推你。好吧,这个好像确实太理所当然、显而易见了,活该存在感不强。
但是我们仔细想想,牛顿第三定律其实是在告诉我们:两个物体相互作用(比如碰撞)时,如果我把它们看作一个整体,那它们之间的作用力就成了内部作用力(以后简称**内力),内力大小相等,方向相反**。
不知道你看到这种大小相等、方向相反的东西有什么反应,会不会有一种想把它们加起来的冲动?
比如,-5和5一点都不好看,但把它们加起来就刚好等于0,消去了,感觉很棒。
代数化简时,看到一堆乱七八糟的东西刚好可以正负抵消,立马心情愉悦。
从经典的俄罗斯方块到现在很火的各类“消消乐”游戏,也都是抓住了人们喜欢看到复杂东西被消去,复杂问题简单化的心理。

那么,既然牛顿第三定律告诉我们相互作用的两个物体间的内力大小相等、方向相反,那我们要不要也来试试,看看能不能玩出一点俄罗斯方块的感觉来?
比如,两个小球在光滑水平面上碰撞时(光滑的意思就是不考虑摩擦力),水平方向上没有其它的外力,主导整个碰撞过程的就是两个小球之间的内力。
根据牛顿第三定律,球A对球B的力,和球B对球A的力大小相等,方向相反。

那么,对待这样两个大小相等、方向相反的内力,我们能做点啥呢?直接把这两个内力加起来,让它们的和等于0**?**
这样做好像没啥意思,直接加起来,得到它们的合力等于0又能说明什么呢?难道用牛顿第二定律F=ma,根据合力去算它们的合加速度?这是两个小球,算一个合加速度,没意义啊。
但是,我们可以把思维拓宽一点,再来观察一下小球的碰撞过程:碰撞的时候,这两个内力大小相等、方向相反,没错。但是,还有一个很隐蔽东西也是相等的,那就是作用的时间t。
两个小球碰撞时间t虽然极短,但它们绝对是相同的。你推了我一秒钟,我当然也反推了你一秒钟,正所谓一个巴掌拍不响。
好,既然两个小球的内力**F和F'大小相等、方向相反(即F+F'=0,力是矢量,正负号代表方向),它们的作用时间Δt又相等。那我把内力和时间乘起来,得到的结果是不是还应该大小相等,方向相反?即:FΔt+F'Δt=0**。
假设两个小球的质量分别为m、m',碰撞过程中加速度分别是a、a*'*,那根据牛顿第二定律F=ma就可以把F、F'写成:F=ma,F'=m'a'。
把F和F'用ma代入上面的式子后,式子就变长了一点:ma**Δt+m'a'Δt=0**。
这个结果很有意思,在maΔt里,原本ma是一组的。但是我们现在棒打鸳鸯,强行把ma拆散,让a和Δt组成新的cp,看看能擦出什么火花。
****
a乘以Δt是什么呢?a是加速度,Δt是碰撞的时间,加速度a乘以时间Δt,这不就是碰撞过程中物体速度的变化量Δv么(加速度a表示单位时间内速度变换了多少,乘以Δt自然就表示Δt时间内速度变化了多少,即:Δv=aΔt)?
这样,我们用牛顿第二定律把F拆成了ma,再把a和后面的Δt组在一起凑成了Δv。那么,原来的式子自然就变成了:m**Δv+m'Δv'=0**。
这个式子就值得玩味了,本来是根据牛顿第三定律,两个内力F和F'大小相等、方向相反:F+F'=0。现在却得到了质量m和速度变化量Δv的乘积mΔv大小相等、方向相反的关系式:mΔv+m'Δv'=0。
我们用一个新的物理量p表示质量m和速度v的乘积,即p**=mv。再给这个p取一个名字,叫动量**。

那么,mΔv自然就表示小球碰撞前后动量**的变化量Δp。于是,原来的mΔv+m'Δv'=0就可以写成Δp+Δp'=0**。
这就意味着,碰撞前后,小球A的动量增加了多少,小球B的动量就要减少多少,这样它们动量的变化量加起来才等于0。
两个物体发生碰撞,碰撞前后,一个物体的动量增加了多少,另一个物体的动量就减少了多少,这说明了什么呢?
这自然说明:碰撞过程中,两个小球的总动量守恒。
30动量守恒定律
碰撞前我们总共有10份动量,碰撞后你的动量增加了2份(+2),我的刚好减少了2份(-2),那总动量还是10份,跟碰撞前一样(2-2=0)。
这就是跟能量守恒定律齐名,另一个大名鼎鼎的守恒律:动量守恒定律。
能量守恒定律更深层的原因是时间平移不变性,就是说昨天的物理定律跟今天的一样;动量守恒定律更深层的原因则是空间平移不变性,就是说北京的物理定律跟武汉的物理定律一样。
****
守恒律跟对称性之间有非常密切的关系,这里我不细说,你们有个概念就行。
再回顾一下推导过程,想想我们是如何得到动量守恒定律的?
我们假设两个小球碰撞时没有摩擦力,也没有其它外力(或者合外力为0),所以它们的内力大小相等、方向相反,再加上作用时间相同,这才得到了动量守恒定律。
也就是说,动量守恒是有条件的,如果我们想让一个系统(比如两个小球)满足动量守恒,那这个系统就必须没有外力(或者合外力为0)作用。
知道了动量守恒,我们再单独看看动量(p=mv)这个概念。
如果我用力**F推一个质量为m的小球,让小球从静止加速到速度v,那它的动量就增加了mv**。
而速度v和加速度a之间有这样一个简单的关系:v=at。我们在两边同时乘以质量m,左边就凑出了动量的样子:mv=mat。右边一眼就看到了ma这个老朋友,立马根据牛顿第二定律F=ma,用力F替换掉。
于是,式子就变成了:mv=Ft。
这个式子告诉我们,我用力F去推一个小球,推了t秒,那么小球的动量(mv)就增加了Ft,动量成了力在时间上的一个累积(还记得力在空间上的累积F·S是什么么?)。
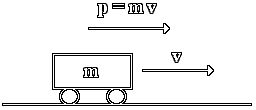
所以,苹果下落时,重力mg就会在时间上不停累积,这就让苹果本身的动量增加了。因为重力对苹果来说是外力,所以苹果自己的动量是不守恒的。
但是,如果我们考虑苹果和地球组成的系统呢?
苹果之所以会下落,是因为地球对苹果有一个引力。这种情况下,让苹果下落的重力就不再是苹果和地球组成系统的外力了,而是系统的内力。
所以,苹果和地球组成的系统,动量就又守恒了。
好,把思路再拓宽一下,你会发现有很多只有内力“窝里横”的场景,这种时候动量守恒定律就会变得非常有用。
****
牛顿第三定律只涉及到作用力和反作用力,孤零零的两个力发挥余地有限。但是,动量的定义是质量乘以速度,速度可是非常基础的物理量啊。
31碰撞
****
再回到经典的碰撞问题上来,如果一个质量为m1的小球以速度v1正面撞击一个质量为m2的静止小球,碰撞之后这两个小球的速度能求出来么?
这是一个非常实在又实用的问题。首先,我们可以想一下:只有这几个条件,能不能求出结果来?
你想啊,一个质量为m1的小球静止在那里,状态是固定的。另一个质量为m2的小球以确定的速度去撞它,这个状态也是确定的。那么,这样撞击之后状态是不是确定的呢?如果把这个过程重复100遍,会得到一样的结果么?
直观的想,结果应该是一样的。如果不一样,就意味着每次用同样的力道去击球,球的速度居然不一样,那台球还怎么玩?

从力的角度考虑,小球以一定的速度去撞击另一个小球,那碰撞产生的力也应该是一样的,于是加速度也一样,所以它的运动状态也应该是一样的。
因此,碰撞后两个小球的速度应该是确定的。**既然确定,你就应该能把它们算出来,算不出来就是没本事**。
那回到问题,对于碰撞过程,碰撞前小球的速度都知道,小球的质量也都知道,唯二不知道的就是两个小球碰撞后的速度。
有两个物理量不知道,我们想求出这两个物理量,就需要找到两个方程(一个方程就是一种限制条件,两个方程才能确定两个未知量,因为两条直线确定一个交点)。
第一个限制条件好说,两个小球发生碰撞(没有外力,不考虑摩擦力),这两个小球组成的系统肯定动量守恒。
假设碰撞后小球的速度分别为v1'和v2',根据动量守恒(碰撞前的总动量等于碰撞后的总动量)就能写出第一个方程:m1×v1+m2×0=m1×v1'+m2×v2'。

于是,我们从动量守恒的角度给出了第一个限制方程。
但是,这个问题有两个未知量v1'、v2',因而需要两个限制方程才能求解,那去哪找第二个方程呢?
很多人立马会想到跟动量守恒齐名的能量守恒,没错,动量和能量确实是看待问题的两个绝佳角度。而且它们都不涉及具体的力,不用分析中间过程,只关注开始状态和最终状态。
因此,我们有理由相信,让动量守恒和能量守恒双剑合璧,应该就能解决问题了。
那么,现在的问题就变成了:小球碰撞过程中能量到底守恒不守恒?不,能量肯定是守恒的,它无非就是从一处跑到了另一处。
由于小球都在地面,它们的能量都以动能(mv²/2)的形式存在。所以,我们更精确的问题应该是:碰撞过程中小球的动能是否守恒?
如果动能也守恒的话,我们立马就可以再列一个方程出来,那两个方程两个未知量,问题就解决了。
由于地面光滑,没有摩擦力,动能没法通过内能损失掉。而碰撞过程中水平方向只有内力在起作用,那这个内力会不会造成小球的动能泄露呢?
32动能是否泄露?
****
回想一下,一个力要如何做才能改变物体动能呢?只要力作用在物体上,物体的动能就会变么?
当然不是!
地面上放着一个大箱子,它的动能为0(因为速度为0)。我用力去推它,结果没有推动,那箱子的动能就还是0,这就说明这个推力没能改变物体的动能。
如果我推动了箱子,让箱子在推力方向上移动了一段距离,那箱子就动了起来,动能就**增加**了。
所以,光有力并不能保证改变物体的动能,我们还需要物体在这个力F的方向上移动了一段距离S,确保F·S≠0之后,才会改变动能。
前面也说了,一个力F作用在物体上,并且使物体在力的方向上移动了一段距离S,物理上就说这个力F对物体做了功。做功是能量由一种形式转化为另一种形式的过程。
这样我们就明白了:要判断小球在碰撞过程中动能是否守恒,关键就要看碰撞时内力到底有没有让小球沿着内力方向移动了一段距离。
简单来说,就是看这个小球有没有被压扁。

因为压扁就是一种形变,碰撞的内力把足球压扁了,就意味着这个内力让足球的一部分在内力的方向上前进了一段距离,所以内力对足球做了功,总动能不再守恒。
33动能守恒的碰撞
****
当然,我们知道世界上并没有绝对坚固的物体,任何物体都是由一大堆分子、原子组成的。两个物体碰撞时,这些分子、原子肯定会动。
但是,考虑到实验的精度,也为了研究的方便,我们还是会考虑这种绝对坚固的刚体。刚体在碰撞时不发生任何形变,内力无法改变它们的动能。
于是,整个碰撞过程就变成了一个小球的动能转移到了另一个小球身上,它们总动能守恒。

所以,如果两个小球是绝对刚体(是不是绝对刚体题目都会告诉你),它们碰撞时没有任何形变,不会被压变形。这种情况下,它们的碰撞过程就不仅满足动量守恒,还满足动能守恒。
于是,我们就可以列出两个方程(动量守恒方程和动能守恒方程),需要求的未知量也只有两个(两个小球碰撞后的速度)。这样,两个方程,两个未知量,直接就能求解了。
另外,我希望大家能够清晰地意识到:到这里,我们这个物理题目就已经做完了。我们根据物理知识分析物理图像,列出了物理方程后,物理工作就做完了,剩下的解方程只是纯数学问题,步骤也是非常程序化的。
大家在学习物理时,对什么是数学问题,什么是物理问题要有清晰的概念。如果你对物理学的框架很熟悉,脑袋中的物理图像也很清晰,那这个界限是很明显的。
****
如果你觉得物理跟数学游戏一样,那就说明还没有建立一个清晰的物理图像,这是很可怕的。

至于为什么有两个未知量,我们就需要列两个方程**,**这是一个非常基础的数学问题。
你想想,如果我们建了一个二维坐标系,两个量(x,y)就组成了坐标系里的一个点。
如果没有任何方程约束它们,那x和y可以取任何值,这个点(x,y)就可以出现在平面的任何一个地方,它们当然是不确定的。
如果有**一个方程呢?那意味着x和y就不能随意取值了,它们的取值必须满足这个方程才行。这样,点(x,y)就只能出现在一些特定的地方,它们就组成了一条直线或者曲线y=f(x)**,也就是函数的图像。
如果有两个方程限制,那(x,y)就必须同时出现在这两条直线(曲线)上,它可以活动的范围就更窄了。如果这两条直线有唯一的交点,这个交点(x,y)就是它唯一可以去的地方,于是x和y就都唯一确定了。
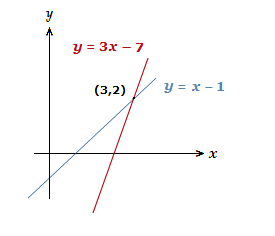
x和y确定了,就意味着未知量都求出来了,那题目也做完了。
这个道理,不清楚的可以自己再琢磨一下。反正,对于物理问题,基本上你有几个未知的物理量,就得列出几个独立的方程来。
所以,你再回头看看小球m1、m2的碰撞过程,它总共有6个物理量:两个小球的质量m1和m2,两个小球碰撞前后各自的速度v1、v2、v1'、v2'。
未知量有6个,但我们拥有的限制方程只有动能守恒和动能守恒2个,6-2=4。
所以,命题老师不管怎么出题,都必须告诉我4个物理量,我才能求出另外2个。如果你只告诉我3个,那对不起,这题解不出来,你另请高明。
为什么只已知3个就一定解不出来呢?还是以碰撞为例,我先告诉你两个小球的质量分别为m1、m2,这已知2个了。再加一个,比如我再告诉你m1碰撞前的速度v1等于0,这就3个了,你能根据这些求出其它物理量么?
这题显然无解啊,两个小球摆在这里,已知一个是静止的,然后你问我它们碰撞之后各自的速度是多少?你确定没有在逗我?
关于物理图像和数学方程之间的事,这里就不多说了。大家可以自己多琢磨琢磨,力求把物理图像搞清楚,然后把一个题目的物理部分和数学部分分清楚,这会大有裨益。
好,两个方程两个未知量,动能守恒的碰撞问题就结束了。
那接下来的问题自然就是:如果不是绝对坚固的小球,如果碰撞时一个小球会被压变形呢?
34动能不守恒的碰撞
****
首先,如果碰撞时小球被压扁了,那碰撞过程中动量还守恒么?答案是动量依然守恒。
因为我们推出动量守恒,只用到了作用力和反作用力大小相等、方向相反,并且作用时间相同。所以,只要没有外力参与,我不管你有没有被压扁(压扁也是内力),总动量都守恒。
但是,如果碰撞时一个小球被压扁了,内力做了功(在力的方向上移动了一段距离),那么碰撞过程中总动能肯定就不再守恒,有一部分动能被内力泄露了出去(比如,挤压小球,小球变热了,动能就转化成了内能)。
如果我们还想从能量守恒的角度也给出一个限制方程,那就必须知道这个内力到底带走了多少能量。也就是必须要能算出这个内力F移动了多少距离S,把F·S算出来**,否则,没戏**。
所以,出题人就不会让你去计算两个皮球撞扁了的情况。因为,把皮球压扁的力F不好算,到底压扁了多大的距离S也不好算(一个球的一半被压扁了,你说这距离要怎么算?)。
于是,你就没法计算内力到底做了多少功,没法知道这个过程中到底损失了多少动能。这样,能量守恒的方程列不出来,就没法算了。
什么,没法算?
那怎么行!出题人有出题人的追求,出题人有出题人的崇高理想。我们怎么能够因为碰撞时损失的动能无法计算就放弃呢?放心,我们一定会想办法让同学们能算出来,而且用中学数学就能算出来。
碰撞问题涉及两个(甚至更多的)物体,比一个物体的问题更复杂。
它可以承载动量守恒、能量守恒这两个极为重要的东西,很全面。而且,如果不是绝对刚体之间的碰撞,动能就还有损失,就更加复杂了,是拉开优等生和特等生好办法,是让高考题具有区分度的绝佳武器。
这么好的机会,错过这个村就没这个店了。出题人不死心,他们在思考:要如何设计,如何简化,才能让这个碰撞问题在高中也能求解呢?
他们想,两个皮球的碰撞问题之所以无法求解,根源就在于碰撞过程损失的动能无法计算,这样能量守恒的方程就列不出来。
皮球碰撞时接触面太大,这样碰撞时就有太多接触点,于是就会有非常多大小不一的力F;接触面积太大,也会让求内力移动的距离S变得遥不可及。
如果想让这个损失的动能F·S可以计算,最好内力F是单一的,而且是可算的。这个碰撞的接触点也不能太多,最好就是一个点。如果碰撞时另一个小球可以变得很小很小,小到跟子弹那样可以近似看成一个点,那子弹打入的深度(即距离S)就好算了,力也相对好求。

咦,那我为什么不干脆就用子弹来出题呢?
于是,出题人就想到利用子弹代替其中的一个小球。至于另一个小球嘛,用子弹打钢球,打不动;用子弹打皮球,会打爆不好控制。于是,出题人想到了一个绝佳的替换物:木块。
子弹打在木块上,木块不会飞,也不会毫发无伤。子弹刚好可以打进木块一定的深度(那这个距离S就搞定了),子弹在木块里受到的力,你说巧不巧,还真有可能是恒力F。
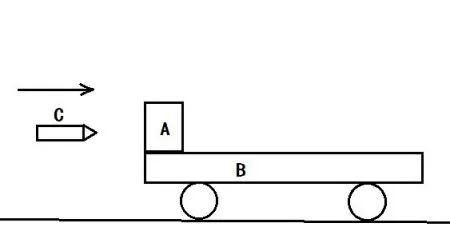
于是,这么一改,力F和距离S就都变得可以计算了,子弹和木块“碰撞”时损失的动能也可以算了(就是子弹打进木块时,子弹和木块的内力和打进深度的乘积)。
那么,左手动量守恒方程,右手能量守恒方程(碰撞前的动能=碰撞后的动能+损失的部分F·S),两个方程两个未知量(碰撞后的速度),剩下就是解方程,纯数学问题了。
于是,大名鼎鼎的“子弹打木块”模型就出来了。
你们看,为了能让你们用高中知识解一道题,出题人也是煞费苦心啊~
35出题与刷题
****
为什么我要在这里给你们剖析出题人的心路历程呢?
如果你能明白为什么“小球碰撞”模型不够用,出题人被迫拉出“子弹打木块”模型来救场,你肯定就能非常明白动量守恒、能量守恒在碰撞过程中的作用。理解了这些,你是不是甚至有点想自己出点题试试了呢?
如果你能理解这些,甚至想自己出出题试试,那基本上就可以告别题海了。

刷题的目的是什么?就是让你通过反复的练习,领悟它们背后的这种关系。如果你已经居高临下地理清了它们之间的逻辑关系,那就只要稍微做点题熟悉一下就完了。
题目是做不完的,题目的变化也是无穷无尽的。但是,所有题目背后的物理规律都是一样的,牛顿力学看待世界的眼光,处理物体运动的方法都是一样的。
我们学习物理,学习牛顿力学,就是要学习它们看待世界,处理运动问题的方法,而不是要陷入无穷无尽的题海中去。
我花如此大精力写这篇文章,当然不是就为了教你几种题目的具体解法(这种书市面上一大堆)。
我是希望能帮你把整个高中物理的内容都串起来,让你在脑海中形成一个清晰、完整的物理图像;让你知道你在分析每一道题,列每一个公式时,知道自己在干什么;让你知道高中物理虽然有定量的计算,但它的整体思想依然是非常简单的。
而且,我也相信你一旦把这体系理清楚了,把这些物理图像都想清楚了,再看到具体题目时,都会有一种“一览众山小”的感觉,觉得题目变来变去也跳不出你的手掌心。
不信的话,我就当你没接触过高中物理,你顺着这篇文章把思路仔细理一理。下一篇文章我就可以带你去看一看、想一想、做一做物理高考题~
好,关于动量的事情就讲到这里。
只要大家能从原理上搞清楚动量是怎么回事,知道动量守恒需要什么条件,知道我们这些过程都是如何推导过来的,脑海里有清晰的物理图像就行了。
当然,虽然我们这里好像是从牛顿第三定律出发“推出”了动量守恒,但这并不是说动量守恒定律就是牛顿第三定律的一个**推论。**
我这个给你“推导”一下,主要是想让你从力的角度对动量守恒有个清晰的图像。
其实,动量、能量远比力用得更广泛,它们在所有物理学里都是非常核心而基础的概念。而力的概念,在牛顿力学之外基本上就没怎么使用了。
****
动量守恒和能量守恒也是在所有物理学里都存在的,决定这些守恒律更深层的原因是时空的**对称性**(能量守恒对应时间平移不变性,动量守恒对应空间平移不变性)。
如果把动量和能量都搞清楚了,把动量守恒和能量守恒的条件和过程也都弄清楚了,那你就掌握了另一种看待物理世界的方法,一种不同于从力的角度看问题的方法。
放心,高中物理不会再有第三种视角了~
36两种视角
****
那么,在分析具体的问题时, 我们是从能量-动量的角度分析,还是从力的角度去分析呢?
一开始的时候,我建议大家两种都试试,正所谓“小孩子才做选择,大人我全都要”。

比如,还是那个自由下落的苹果。
从力的角度看,是苹果受到的合外力为重力。在重力的作用下,苹果按照牛顿第二定律F=ma产生了一个重力加速度(大小约为9.8m/s²),然后苹果以这个加速度运动。至于运动的具体细节,不过就是那5个运动物理量(V0、Vt、a、t、S)之间的数学关系。
从能量的角度看,就是苹果的重力势能转化成了动能。因为总能量是守恒的,所以,重力势能减少了多少,相应动能就会增加多少。
从动量的角度看,苹果下落时受到了一个外力(重力),所以苹果的动量是增加的。
但是,如果你把苹果和地球看作一个整体,那重力就成了苹果和地球之间的内力,那么苹果-地球组成的系统就动量守恒了。但这好像也没啥用,地球对苹果来说太大了,我们也没有无聊到想去计算一个苹果下落对地球运动造成的影响(起码等苹果有月亮那么大再说)。

同样,一个小球从光滑斜面上滚下来,你可以对它进行受力分析,利用F=ma计算它的加速度,分析它的运动情况,也可以看成是它的重力势能转化成了动能。
如果斜面不光滑,有摩擦力,那你在计算合力时就要把摩擦力考虑进去,考虑能量转化的时候也要把摩擦力做的功考虑进去。
不管这个力怎么变,从重力变成一个推力、摩擦力、电场力、弹力等等都好,上面这个思路并不会变。从力的角度来看,无非就是变换了一个力的品种,从能量的角度来看,不过就对应增加了一种能量,它们之间是一一对应的。
如果两种思路都玩熟了,你自然就知道在什么样的情况下选择什么样的思路会更简单,而不用一开始就牢记某种所谓的“简便”方法。
这种不明白大局的“简便”,往往是最复杂的。就像一个武林高手可以谈“无招胜有招”,你在新手村谈“无招胜有招”就是找死。
37物理与数学
****
此外,我们在分析物理过程时,要尝试把问题的物理部分和数学部分区分开。
说简单一点就是,当我从物理角度,从力或者能量-动量的角度考虑问题时,我把方程列出来就算完了,剩下解方程只是数学问题。
不过,我们心里要明确:一个方程其实就是一种限制。
一个苹果在没有任何限制的时候,它可以随便动。但是,因为它下落时要满足能量守恒,这个能量守恒就是一种限制。因为这种限制,苹果就只能那样下落。
如果我们要求的未知量只有一个,那只需要一个方程就能把未知量求出来(比如求苹果下落的末速度,能量守恒一个方程即可);如果我们要求的未知量有两个,那就需要两个方程才能把未知量都求出来(比如小球碰撞时,求两个小球的末速度,就需要从能量、动量的角度各找一个方程)。
把方程找齐了,这个物理题目就算做完了,因为解方程不属于物理过程,它有非常固定的数学解法。
所以,我希望大家在学习高中物理时,能先把整个框架,整个脉络理清楚,把物理过程的图像都看清楚。在这个基础之上,我们再去追求所谓的简便方法,各种技巧,这也是我写这篇文章的原因。

很多人一到高中就钻进各种各样的技巧和简便方法里去了,他记住了各种物理模型,知道碰到这种题应该怎么做,碰到那种题应该怎么做。但是,他无法通过这些题目建立起一个完整的力学图景来,无法让他的知识点变成知识体系。
这样,题目一变,题型一变,他就会感觉很吃力。然而,无论出题老师怎么变,在高中玩力学,都逃不出牛顿的手掌心。
这个道理,希望大家能早点明白。
38结语
****
长尾君本来是在写相对论的,上一篇文章还是《》。按照原先的计划,我是打算等相对论-量子力学-量子场论之类的写完了再来写中学物理的。
但是,社群里有些家长的孩子已经高中了,有些快要念高中了。他们很希望我能尽快写点中学物理的东西,从更高的维度把高中物理串起来(就像之前的主线文章那样)。
还有些家长,虽然孩子还在念小学,但从小的科普书、科普视频没少看,能够定性的从大爆炸、黑洞、引力讲到电子、中子星、夸克。他们从小对科学非常感兴趣,家长也很高兴。
但是,当孩子们好像什么都能定性地说一点时,家长们反倒不知道接下来应该怎么办了。
因为很多东西定性了解起来容易,但是如果想继续深入了解,就得知道如何做定量计算。这本来是从初中物理到高中物理的转变,但由于现在获取信息变容易了,很多小学生也面临这种问题。
这也很容易让有些小学生形成一种错觉:让他们觉得物理好像也不过如此,觉得自己好像已经天上地上什么都知道了,然后开始自大……
我一直把中小学生的科学教育看得非常重要,之前的、、系列文章,我都执意把它们写得极为通俗(以至于让有些读者觉得太啰嗦),目的就是尽量让更多人,包括中小学生也能看懂。
****
即便中小学生看起来太费劲,或者没有机会看公众号的文章,家长们看懂之后按照这个思路也能很容易给孩子讲明白。
科学教育要从孩子抓起,只有小孩子真正理解科学,热爱科学,我们才能诞生真正的科学大师,这个道理大家都懂。

所以,我还是决定先暂停相对论的科普工作,转而写一篇帮大家理清高中物理框架,建立物理图像的文章。虽然这种文章的B格没有相对论、量子力学那么高,但是,我想应该会有更多中小学生从中受益吧。
社群里有位大佬回忆他的初中物理老师时,有句话让我印象非常深刻,他的老师说:“我先教你们什么是真正的物理,再用半年教你们如何应付考试。”
帅呆了有木有?这也是我想通过这篇文章传递给你们的一个信息。
我知道很多人进入高中以后,会开始觉得物理很枯燥、很难,觉得它既不酷又不美。
****
但这不是物理的错,而是你看待物理的角度错了。
我们欣赏一处风景,看一部电影,都有一个正确的打开方式。你躲在一个山洞里,当然无法欣赏“登高壮观天地间,大江茫茫去不还”的壮丽;你在电影院第一排的最角落,当然也很难很好地欣赏一部电影了。
你想想,牛顿、爱因斯坦、狄拉克这些人为什么会被物理学迷得死去活来?再想想,你学的物理跟他们学的物理并没有什么不一样啊?
所以,物理学本身是非常美的,需要改变的并不是物理本身,而是我们看待物理的眼光。

我也学过高中物理,所以很清楚许多人到了高中是如何把物理看歪了的,希望这篇文章能多多少少帮大家把角度扶正一点。
最后,高中物理并不是对初中物理和科普物理的“背叛”,而是一种深化,物理学的内核始终是一致的。能够进行定量计算的物理,就像老酒一样,越品越醇,越品越香。